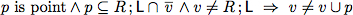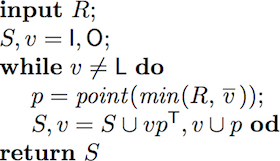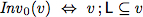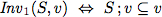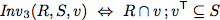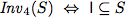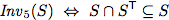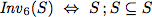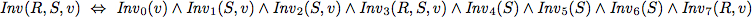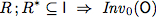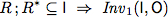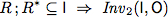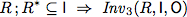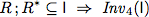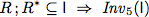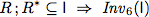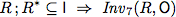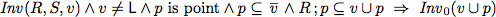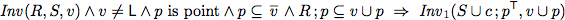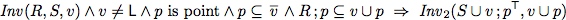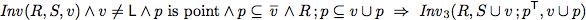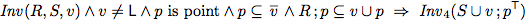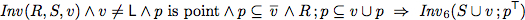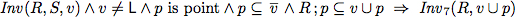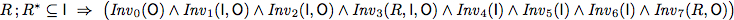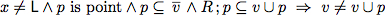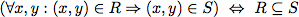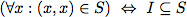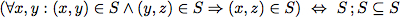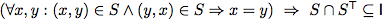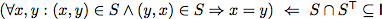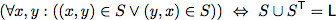Automated Verification of Relational While-Programs
R. Berghammer, P. Höfner, I. Stucke
Abstract: Software verification is essential for safety-critical systems. In this paper, we illustrate that some verification tasks can be done fully automatically. We show how to automatically verify imperative programs for relation-based discrete structures by combining relation algebra and the well-known assertion-based verification method with automated theorem proving. We present two examples in detail: a relational program for determining the reflexive-transitive closure and a topological sorting algorithm. We also treat the automatic verification of the equivalence of common-logical and relation-algebraic specifications.
Paper: pdf
Reflexive-transitive Closure
The first algorithm we are going to verify with the help of Prover9 is an algorithm for computing the reflexive-transitive closure for a given relation.
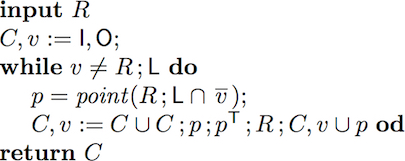
To verify this algorithm we establish two invariants.
| Invariants |
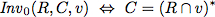 |
 |
Prover9 can verify partial correctness of this algorithm, using the following input files (for more details, we refer to the paper). Next to the input files, we also list running times.
The first law of maintenance could not be proven with our standard input file.We had to add three auxiliary facts about the Kleene star.However, all these facts could be proven fully automatically without any interaction.
So far we have established partial correctness of the algorithm.However, for this algorithm we can even show total correctness with the help of Prover9.For this proof the following properties are sufficient.
1In this example Prover9 finds a proof, but outputs "SEARCH FAILED"followed by "Exiting with 1 proof" (or some other number).A close inspection of the proof logs showed that such situations occur in case negative clauses are included in the goals.Then the output is misleading, since in such cases Prover9 did find a proof, but thought it had to keep searching
Topological Sorting of Noetherian Relations
The second algorithm we verify is an algorithm for topological sorting.
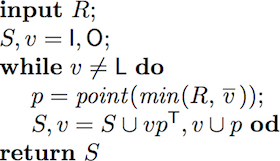
To verify this algorithm we establish two invariants.
As abbreviation we use
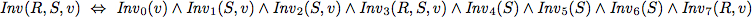
Prover9 can verify partial correctness of this algorithm, using the following input files (for more details, we refer to the paper).
The establishment of the invariants can be done without splitting:
So far we have established partial correctness of the algorithm.However, for this algorithm we can again total correctness; it is similar to the above.
Equivalence of Logical and Relation-algebraic Specifications
Above we have automatically proven total correctness for two relational while programs. One reason why we could use automated theorem provers is that we are able to write program specifications as relational expressions. However, often specifications and program properties are
not given in a relation-algebraic manner;but in predicate-logic. Luckily, it is easy to show equivalences between logical and relation-algebraic specifications.
Note: The relation-algebraic expression inside the tables follow the paper and use the same notation; the input files, however, often make use of Prover9's feature of "automated quantifying". This feature only works for variables named u,v,w,x,y and z. That is why the input files sometimes use different variable names.
Contact: Peter Höfner: peter <at> hoefner-online.de
Last update: 2013
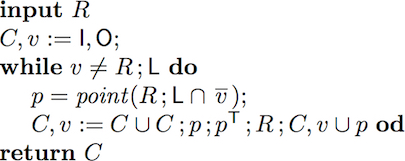
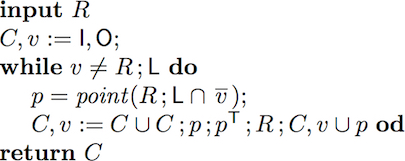
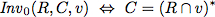

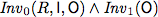
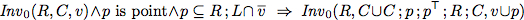
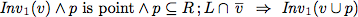

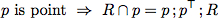
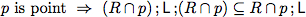
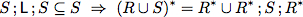

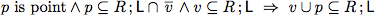
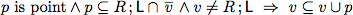 1
1